Automaattinen tarkistus
Rakenteisten päättelyketjujen editoriin voi liittää lisäosan, jonka avulla voi tarkistaa, onko päättelyketju matemaattisesti oikein. Tarkistin muotoilee jokaisen päättelyketjun askeleen teoreemaksi, jonka se lähettää pilvipalvelimessa toimiville automaattisille teoreematarkistimille. Päättelyketju on oikein, jos sen jokainen askel voidaan todistaa.
Virheellinen päättelyketju
Seuraava päättelyketju on virheellinen, sillä toisessa askeleessa on laskuvirhe. Tarkistin merkitsee huutomerkin (!) virheellisen askeleen kohdalle, ja ٪ - merkin oikein tehtyjen askelten kohdalle.
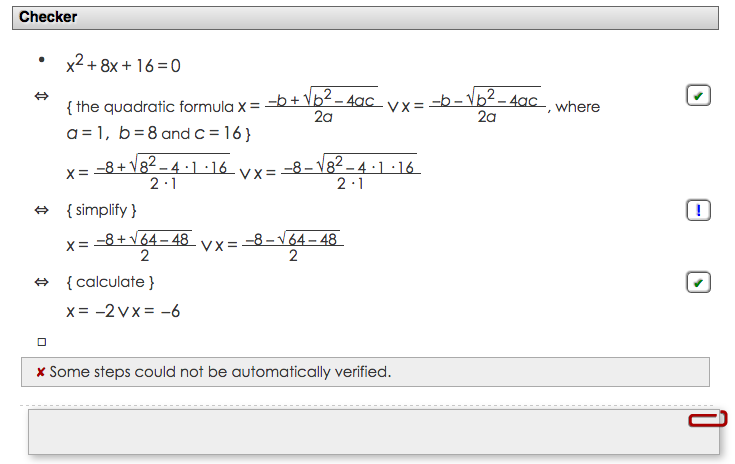
Korjattu päättelyketju
Tässä virhe on korjattu. Tarkistin merkitsee kaikki askeleet oikein tehdyiksi, joten koko päättelyketju on oikein.
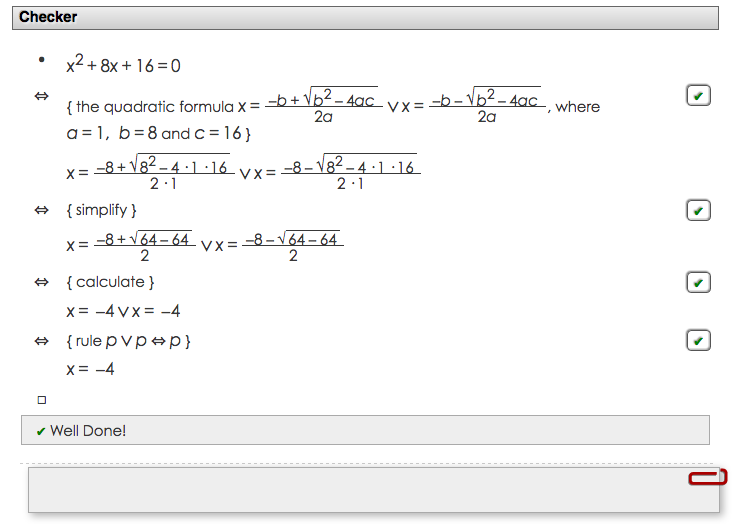
Tarkistimen käyttö
Tarkistin jättää jokaiseen askeleeseen sarakkeen oikeaan reunaan merkin.
- Tarkistin voi ilmoittaa, ettei se ymmärrä askelta, jolloin se pitää kirjoittaa uudelleen:
- - Askeleessa voi olla syntaksivirhe, ja se pitää korjata.
- - Tarkistin ei ymmärrä merkintätapaa. Tällöin pitää käyttää toisenlaista merkintätapaa.
- Tarkistin voi ilmoittaa askeleen oikeaksi. Askel on kunnossa.
- Tarkistin ymmärtää askeleen, muttei pysty todistamaan sitä.
- - Askel voi olla virheellinen, jolloin sitä ei voi todistaa. Virhe pitää korjata.
- - Askel voi olla oikein, mutta tarkistin ei pysty todistamaan sitä käytettävissä olevassa ajassa. Sen voi yrittää pilkkoa pienempiin askeleisiin.
- - Askel voi olla oikein, mutta tarkistimella ei ole riittävästi tietoa sen todistamiseen. Tällöin tarkistimelle pitää antaa lisää tietoa oletuksissa, johdettuina tosiasioina tai määritelminä.
Tarkistin on vain päättelyketjujen tarkistamisen apuväline. Se voi kuitenkin antaa hyviä vihjeitä siitä, miten ongelma ratkaistaan oikein.

Mitä tarkistin voi todistaa?
Rakenteisten päättelyketjujen automaattinen tarkistin käyttää useita automaattisia teoreematodistimia rinnakkain yrittäessään todistaa askeleen oikeaksi. Kaikilla teoreematodistimilla on omat erityisalueensa, ja jokainen niistä voi olla hyvä yhdessä asiassa mutta huono toisessa. Tarkistimen tehokkuus riippuu siis siitä, onko juuri kyseiselle osa-alueelle tehokas todistin käytössä.
Osaamisalueet
Automaattinen tarkistin on varsin hyvä seuraavilla matematiikan osa-alueilla:
- polynomit (yhtälöt, epäyhtälöt, funktiot)
- rationaalilausekkeet (aritmeettiset ja polynomiset lausekkeet)
- juurilausekkeet (potenssit, neliöjuuret, murtopotenssit)
- logaritmit
- eksponenti
- ensimmäisen kertaluvun logiikka
- perustrigonometria
Jotkin näistä osa-alueista voivat vaatia tavallista tehokkaampia todistimia, jotka ovat käytössä lisämaksusta.
Automaattinen tarkistimen käyttö
Automaattinen tarkistin on käytettävissä 4f Studiossa sekä 4f Notessa. Sitä voi käyttää missä tahansa matematiikkaeditoria käytetään: 4f Note-sivulla, 4f Studion oppikirjassa tehtävää ratkaistaessa, 4f Studio vihkossa sekä 4f Studio kurssikirjassa. Tarkistin vaatii toimiakseen verkkoyhteyden sekä käyttökiintiö. Ratkaisun voi tarkistaa valitsemalla valikosta ”Tarkista”. Tämä käynnistää tarkistusprosessin.

